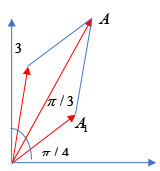
Dao động của một là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {2t + \frac{\pi }{4}} \right)cm;{x_2} = 3\cos (2t + \varphi )cm(t\) tính bằng \(s),{A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)cm\). Độ lớn gia tốc lớn nhất của vật là

D. \(23,2\;cm/{s^2}\).

\(A_2^2 = 9 = {A^2} + A_1^2 - 2.A.{A_1}cos(\frac{\pi }{3} - \frac{\pi }{4})\)=> \(A_1^2 - 2.A.{A_1}cos(\frac{\pi }{3} - \frac{\pi }{4}) + {A^2} - 9 = 0\)

Để phương trình có nghiệm thì

\(\Delta = {(2.A.cos{15^0})^2} - 4({A^2} - 9) \ge 0\)=> \(A \le \frac{3}{{\sin {{15}^0}}} = 11,6\)

=> \({a_{max}} = {\omega ^2}A \le 46,4\)