Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x² – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?

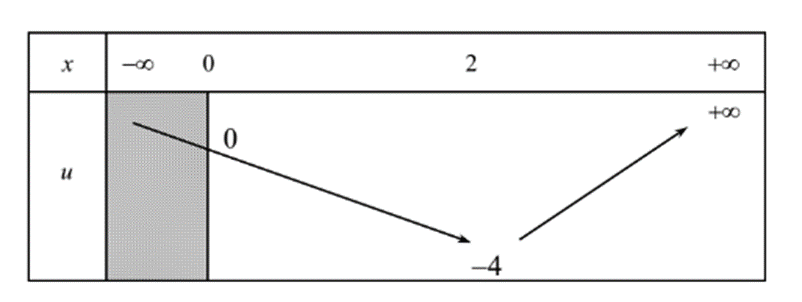
Ta thấy:

+) Với u < –4, phương trình (1) vô nghiệm

+) Với u = –4, phương trình (1) có một nghiệm x = 2 > 0

+) Với –4 < u < 0, phương trình (1) có hai nghiệm x > 0

+) Với u ≥ 0, phương trình (1) có một nghiệm x > 0

Khi đó 3f(x² – 4x) = m             

\( \Rightarrow f\left( u \right) = \frac{m}{3}\)                  (2)

Ta thấy:

+) Nếu \(\frac{m}{3} = - 3 \Leftrightarrow m = - 9\) thì phương trình (2) có một nghiệm u = 0

Nên phương trình (1) có một nghiệm x > 0

+) Nếu \( - 3 < \frac{m}{3} < - 2 \Leftrightarrow - 9 < m < - 6\) thì phương trình (2) có một nghiệm u > 0 và một nghiệm u ∈ (–2; 0)

Nên phương trình (1) có ba nghiệm x > 0

+) Nếu \(\frac{m}{3} = - 2 \Leftrightarrow m = - 6\) thì phương trình (2) có một nghiệm u = –4, một nghiệm u ∈ (–2; 0) và một nghiệm u > 0

Nên phương trình (1) có bốn nghiệm x > 0

+) Nếu \( - 2 < \frac{m}{3} < 2 \Leftrightarrow - 6 < m < 6\) thì phương trình (2) có một nghiệm u < –4, hai nghiệm u ∈ (–4; 0) và một nghiệm u > 0

Nên phương trình (1) có năm nghiệm x > 0

+) Nếu \(\frac{m}{3} = 2 \Leftrightarrow m = 6\) thì phương trình (2) có một nghiệm u < –4, một nghiệm u = –2 và một nghiệm u > 0

Nên phương trình (1) có ba nghiệm x > 0

+) Nếu \(\frac{m}{3} > 2 \Leftrightarrow m > 6\) thì phương trình (2) có một nghiệm u < –4 và một nghiệm u > 0

Nên phương trình (1) có một nghiệm x > 0

Suy ra –9 < m ≤ 6

Do đó m ∈ {–8; –7; –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6}

Vậy ta chọn đáp án A.