Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x³ – 3(m + 2)x² + 3(m² + 4m)x + 1 nghịch biến trên khoảng (0; 1)?

A. 1;

B. 4;

C. 3;

D. 2.

Đáp án đúng là: B

Ta có: y’ = 3x² – 6(m + 2)x + 3(m² + 4m)

Khi đó y’ = 0 ⇔ 3x² – 6(m + 2)x + 3(m² + 4m) = 0

⇔ x² – 2(m + 2)x + m² + 4m = 0 (1)

Ta có: ∆’ = (m + 2)² – (m² + 4m) = 4 > 0

Nên phương trình (1) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = m\\x = m + 4\end{array} \right.\)

Bảng biến thiên:

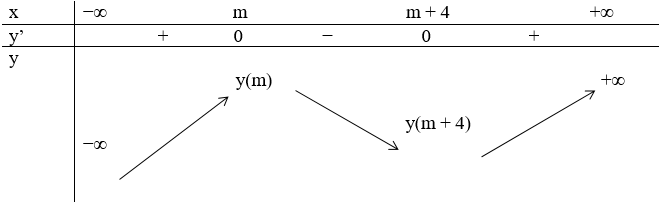
Từ bảng biến thiên, ta suy ra để hàm số nghịch biến trên khoảng (0; 1)

⇔ (0; 1) ⸦ (m; m + 4) \( \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m + 4 \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 3\end{array} \right.\)⇔ −3 ≤ m ≤ 0

Mà m ∈ ℤ nên m ∈ {−3; −2; −1; 0}.

Vậy có 4 giá trị của m thỏa mãn yêu cầu bài toán.