Chứng minh rằng trong mọi tam giác ABC ta đều có: a) a = b cosC + c cosB
Chứng minh rằng trong mọi tam giác ABC ta đều có:
a) a = b cosC + c cosB;
b) sinA = sinBcosC + sinCcosB;
c) ha = 2RsinBsinC.
a) Áp dụng hệ quả của định lí cosin trong tam giác ta có
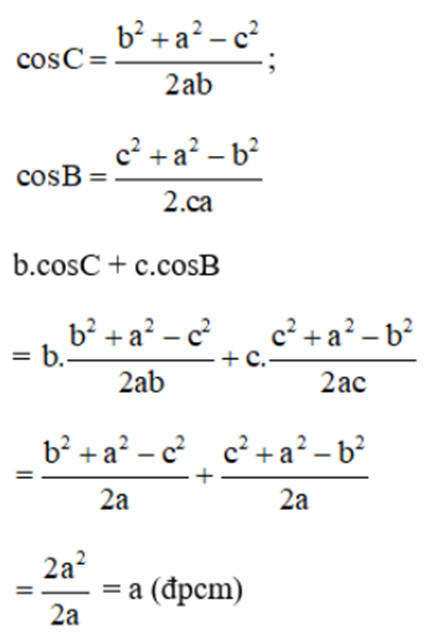
Vậy a = b cosC + c cosB
b) Theo định lí tổng ba góc trong một tam giác có
\(\widehat A + \widehat B + \widehat C = 180^\circ \)
Hay \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right)\)
Suy ra \(\sin A = \sin \left( {180^\circ - \left( {\widehat B + \widehat C} \right)} \right) = \sin \left( {B + C} \right)\) = sinBcosC + cosBsinC.
Vậy sinA = sinBcosC + sinCcosB
c) Áp dụng hệ quả của định lí sin trong tam giác ta có
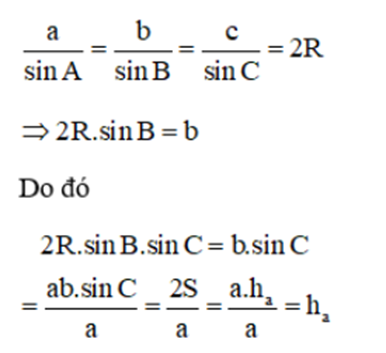
Vậy ha = 2RsinBsinC.