Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ .

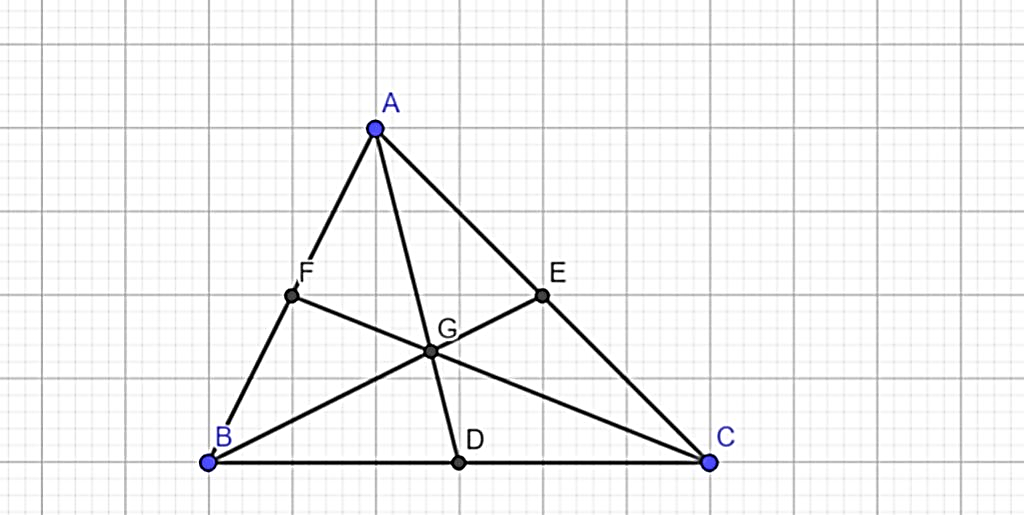
Gọi D, E, F là trung điểm BC, AC, AB

* Chứng minh G là trọng tâm của tam giác ABC thì $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GA}+\left(\overrightarrow{GB}+\overrightarrow{GC}\right)=\overrightarrow{GA}+2\overrightarrow{GD}$  (Vì D là trung điểm BC)

Mà G là trọng tâm của tam giác ABC nên GA = 2GD

Suy ra: $\overrightarrow{GA}=-2\overrightarrow{GD}$ ⇒ $\overrightarrow{GA}+2\overrightarrow{GD}=\overrightarrow{0}$

⇒ $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

* Chứng minh $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$  thì G là trọng tâm của tam giác ABC.

Ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

⇒ $\overrightarrow{GA}+\left(\overrightarrow{GB}+\overrightarrow{GC}\right)=\overrightarrow{0}$

⇒ $\overrightarrow{GA}+2\overrightarrow{GD}=\overrightarrow{0}$

⇒ $\overrightarrow{GA}=-2\overrightarrow{GD}$

⇒ A, G, D thẳng hàng; G nằm giữa A và D; GA = 2GD

Mà AD là trung tuyến của tam giác ABC

Suy ra: G là trọng tâm của tam giác ABC.