Chứng minh các hệ thức a) 1 + tan^2 a = 1/cos^2 a b) 1 + cot^2 a = 1/sin
Chứng minh các hệ thức
a) 1+tan2a=1cos2a;
b) 1+cot2a=1sin2a;
c) cosa1−sina=1+sinacosa.
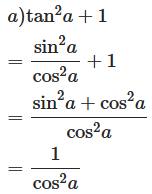
Vậy 1+tan2a=1cos2a.
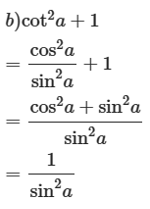
Vậy 1+cot2a=1sin2a.
c) cosa1−sina=1+sinacosa
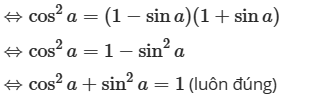
Vậy cosa1−sina=1+sinacosa.