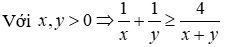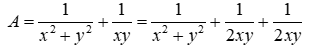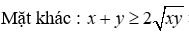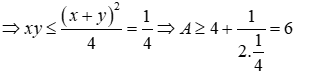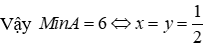Cho x, y > 0 và x + y = 1. Tìm GTNNcura biểu thức A = 1 / (x^2 + y^2) + 1/xy
Cho \(x,y > 0\)và \(x + y = 1.\)Tìn GTNN của biểu thức \(A = \frac{1}{{{x^2} + {y^2}}} + \frac{1}{{xy}}\)
Cho \(x,y > 0\)và \(x + y = 1.\)Tìn GTNN của biểu thức \(A = \frac{1}{{{x^2} + {y^2}}} + \frac{1}{{xy}}\)