Cho tứ giác MNPQ ( hình bên ) . Ba điểm E, F, K lần lượt là trung điểm của
41
27/08/2024
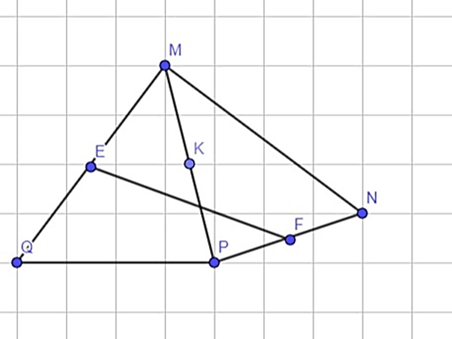
Cho tứ giác MNPQ ( hình bên ) . Ba điểm E, F, K lần lượt là trung điểm của MQ, NP và MP. Kết luận nào sau đây đúng?
A. \(EF = \frac{{MN + PQ}}{2}\).
B. \(EF \le \frac{{MN + PQ}}{2}\).
C. \(EF < \frac{{MN + PQ}}{2}\).
D. \(\frac{{MN + PQ}}{2} > 2\).
Trả lời
Đáp án đúng: B
Vì E, K là trung điểm của MQ và QP nên EK là đường trung bình của tam giác MQP
Suy ra: \(EK = \frac{{QP}}{2}\)
Tương tự: KF là đường trung bình của tam giác MNP
Suy ra: \(FK = \frac{{MN}}{2}\)
Khi E,K, F thẳng hàng thì EK + KF = EF
⇔ EF = \(\frac{{QP}}{2} + \frac{{MN}}{2} = \frac{{MN + PQ}}{2}\)(1)
Khi E, K, F không thẳng hàng. Áp dụng bất đẳng thức tam giác cho tam giác EKF có:
EK + KF > EF
⇔ EF < \(\frac{{MN + PQ}}{2}\)(2)
Kết hợp (1) và (2) suy ra: \(EF \le \frac{{MN + PQ}}{2}\).