Cho tứ giác lồi ABCD có AB = BC = CD = a, góc BAD = 75 độ, góc ADC = 45 độ
Cho tứ giác lồi ABCD có AB = BC = CD = a, \(\widehat {BAD} = 75^\circ ;\widehat {ADC} = 45^\circ \). Tính độ dài AD?
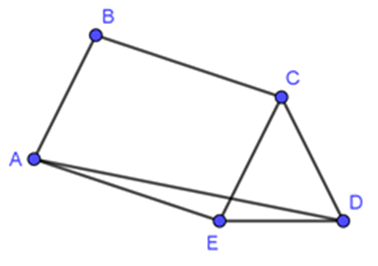
Xét \({T_{\overrightarrow {BC} }}\left( A \right) = A'\)
Khi đó: CA' = BA = CD, suy ra tam giác CA'D cân tại C'
⇒ \(\widehat {A'CD} = 60^\circ \)⇒ ∆CA'D đều
⇒ \(\widehat {A'DA} = 15^\circ \)và AA' = BC = CD = A'D = a
⇒ \(\widehat {AA'D} = 150^\circ \)
Do đó: AD2 = 2A\('\)A2 – 2A\('\)Acos\(\widehat {AA'D}\) = 2a2 + \(\sqrt 3 {a^2}\)
Suy ra: AD = \(a\sqrt {2 + \sqrt 3 } \).