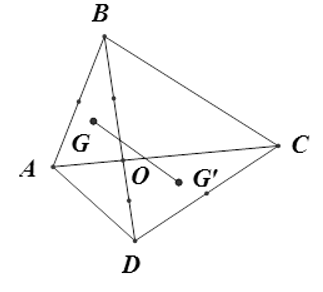
Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto .

28 19/08/2024

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto $\vec{G G^{'}}$ .

Trả lời

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto . (ảnh 1)

Vì G’ là trọng tâm của tam giác OCD nên $d = \frac{a \sqrt{6}}{6}$ (1)

Vì G là trọng tâm của tam giác OAB nên $\vec{G O} + \vec{G A} + \vec{G B} = \vec{0}$

Khi đó $\vec{G O} = - \vec{G A} - \vec{G B}$ .

Từ (1) và (2) suy ra $\vec{G G^{'}} = \frac{1}{3} (- \vec{G A} - \vec{G B} + \vec{G C} + \vec{G D}) = \frac{1}{3} (\vec{A C} + \vec{B D})$

Vậy $\vec{G G^{'}} = \frac{1}{3} (\vec{A C} + \vec{B D})$ .

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

Câu hỏi cùng chủ đề

Cho alpha và beta là hai góc nhọn bất kỳ thỏa mãn alpha + beta = 90 độ

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

30 1 tháng trước

Trong mặt phẳng (Oxy) cho A(1; 2), B(4; 1), C(5; 4). Tính góc BAC A. 60 độ B. 45 độ

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

26 1 tháng trước

Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

30 1 tháng trước

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

24 1 tháng trước

Cho tam giác ABC và đặt vecto a = vecto BC, vecto b = vecto AC. Cặp vecto nào sau đây

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

25 1 tháng trước

Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

25 1 tháng trước

Bất phương trình log(2/3) (2x^2 - x - 1) > 0 có tập nghiệm là (a; b) hợp (c; d)

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

25 1 tháng trước

Cho phương trình log 2 2 x - 2 log2 x - căn bậc hai (m + log2 x) = m (*). Có bao nhiêu

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

24 1 tháng trước

Gieo ba con súc sắc. Xác suất để được nhiều nhất hai mặt 5 là A. 5/72 B. 1/216

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

24 1 tháng trước

Các yếu tố nào sau đây xác định một mặt phẳng duy nhất A. Hai đường thẳng

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

23 1 tháng trước

Xem tất cả

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto .

Trả lời

Câu hỏi cùng chủ đề

Cho alpha và beta là hai góc nhọn bất kỳ thỏa mãn alpha + beta = 90 độ

Trong mặt phẳng (Oxy) cho A(1; 2), B(4; 1), C(5; 4). Tính góc BAC A. 60 độ B. 45 độ

Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a

Cho tam giác ABC và đặt vecto a = vecto BC, vecto b = vecto AC. Cặp vecto nào sau đây

Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5

Bất phương trình log(2/3) (2x^2 - x - 1) > 0 có tập nghiệm là (a; b) hợp (c; d)

Cho phương trình log 2 2 x - 2 log2 x - căn bậc hai (m + log2 x) = m (*). Có bao nhiêu

Gieo ba con súc sắc. Xác suất để được nhiều nhất hai mặt 5 là A. 5/72 B. 1/216

Các yếu tố nào sau đây xác định một mặt phẳng duy nhất A. Hai đường thẳng

Danh mục