Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo (không vuông góc), I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K. a) C
31
12/05/2024
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo (không vuông góc), I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K.
a) Chứng minh rằng tứ giác BMND là hình bình hành.
b) Với điều kiện nào của hai đường chéo AC và BD thì tứ giác BMND là hình chữ nhật?
c) Chứng minh ba điểm M, C, N thẳng hàng.
Trả lời
Lời giải
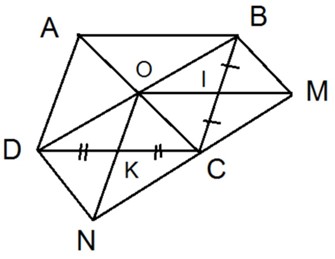
a) Ta có \[\left\{ \begin{array}{l}BH = HC\\MH = HO\end{array} \right.\]
Suy ra tứ giác BMND là hình bình hành
Do đó \[\left\{ \begin{array}{l}BM\parallel OC\\BM = OC\end{array} \right.\] (1)
Tương tự, tứ giác OCND là hình bình hành.
Suy ra \[\left\{ \begin{array}{l}DN\parallel OC\\DN = OC\end{array} \right.\] (2)
Từ (1) và (2) suy ra \[\left\{ \begin{array}{l}BM\parallel DN\\BM = OC = DN\end{array} \right.\]
Do đó tứ giác BMND là hình bình hành.
b) Ta có BMND là hình bình hành (câu a) trở thành hình chữ nhật thì BM // AC.
Vậy để BMND là hình chữ nhật thì BM // AC
c) Vì BMCO là hình bình hành nên MC // BD (3)
Và BMND là hình bình hành nên MN // BD (4)
Từ (3) và (4) suy ra M, N, C thẳng hàng (theo tiên đề Ơ–clit).

