Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. a) Chứng minh vecto MN = 1/2 (vecto AB + vecto DC). b) Xác định điểm O sao cho
81
18/05/2024
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC.
a) Chứng minh →MN=12(→AB+→DC).
b) Xác định điểm O sao cho →OA+→OB+→OC+→OD=→0.
Trả lời
Lời giải
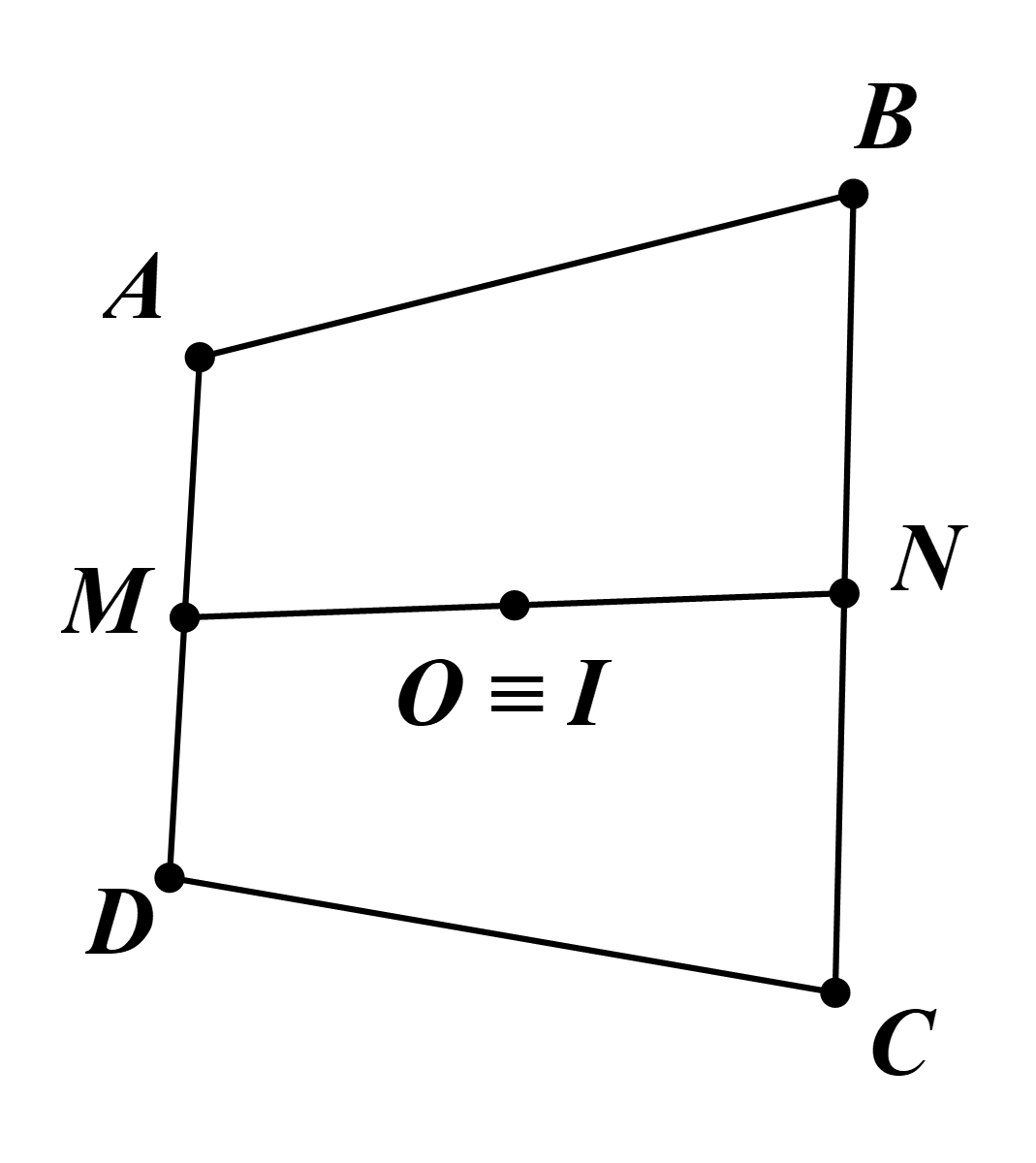
a) Ta có VT=→MN=12(→MA+→AB+→BN)+12(→MD+→DC+→CN)
=12(→MA+→MD)+12(→BN+→CN)+12(→AB+→DC) (M, N lần lượt là trung điểm của DA, BC).
=12.→0+12.→0+12(→AB+→DC)=12(→AB+→DC)=VP.
Vậy ta có điều phải chứng minh.
b) Ta có →OA+→OB+→OC+→OD=→OA+→OD+→OC+→OB
=2→OM+2→ON=2(→OM+→ON)=4→OI, với I là trung điểm MN.
Khi đó →OA+→OB+→OC+→OD=→0⇔→OI=→0.
Tức là, O ≡ I.
Vậy O ≡ I thỏa mãn yêu cầu bài toán.

