Cho tứ giác ABCD có O là giao điểm hai điểm hai đường chéo và diện tích tam giác AOB bằng 4, diện tích tam giác COD bằng 9. Tìm giá trị nhỏ nhất của diện tích tứ giác ABCD.

Trả lời

Lời giải

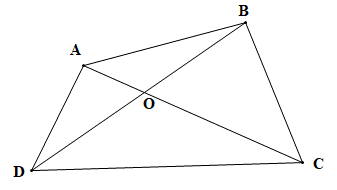
Đặt S_AOD = x, S_BOC = y

Ta có \(\frac{{{S_{AO{\rm{D}}}}}}{{{S_{CO{\rm{D}}}}}} = \frac{{AO}}{{OC}}\), \(\frac{{{S_{AOB}}}}{{{S_{COB}}}} = \frac{{AO}}{{OC}}\)

Suy ra \(\frac{{{S_{AO{\rm{D}}}}}}{{{S_{CO{\rm{D}}}}}} = \frac{{{S_{AOB}}}}{{{S_{COB}}}}\)

Hay \(\frac{x}{9} = \frac{4}{y}\)

Suy ra xy = 36

\[{S_{ABC{\rm{D}}}} = {S_{AOB}} + {S_{BOC}} + {S_{CO{\rm{D}}}} + {S_{AO{\rm{D}}}} = 4 + y + 9 + x = x + y + 13\]

Suy ra \[{S_{ABCD}} \ge 2\sqrt {xy} + 13\]

Nên \[{S_{ABCD}} \ge 2\sqrt {36} + 13\]

Hay S_ABCD  ≥ 25

Dấu bằng xảy ra khi x = y = 6

Vậy diện tích tứ giác ABCD nhỏ nhất bằng 25 khi S_AOD = S_BOC = 6.