Cho tứ giác ABCD có M, N, P, Q, E, F là trung điểm của AB, BC, CD, DA, AC, BD. Chứng minh:

a) MN = PQ và NP = MQ.

b) MF = PE và ME = PF.

c) Tứ giác MEPF và tứ giác MNPQ là hình bình hành.

Lời giải

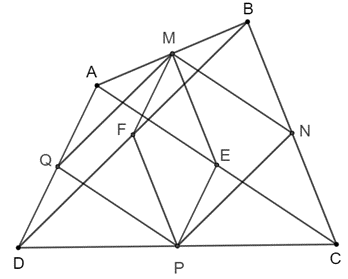
a) * Xét ΔBAC có:

• AM = MB (vì M là trung điểm AB);

• BN = NC (vì N là trung điểm CB).

Do đó MN // AC; $MN = \;\frac{1}{2}AC$ (định lí đường trung bình của một tam giác) (1)

* Xét ΔACD có:

• AQ = QD (vì Q là trung điểm AD);

• CP = PD (vì P là trung điểm CD).

Do đó PQ // AC; $QP = \;\frac{1}{2}AC$ (định lí đường trung bình của một tam giác) (2)

Từ (1) và (2) suy ra MN // PQ // AC; $MN = PQ = \;\frac{1}{2}AC$.

* Xét ΔBCD có:

• CN = NB (vì N là trung điểm CB);

• CP = PD (vì P là trung điểm CD).

Do đó NP // BD; $NP = \;\frac{1}{2}BD$ (định lí đường trung bình của một tam giác) (3)

* Xét ΔABD có:

• AM = MP (vì M là trung điểm AB)

• AQ = QD (vì Q là trung điểm AD)

Do đó  MQ // BD; $MQ = \frac{1}{2}BD$ (định lí đường trung bình của một tam giác) (4)

Từ (3) và (4) suy ra NP // MQ // BD;  $NP = MQ = \;\frac{1}{2}BD$. 

b) * Xét ΔABD có:

• MA = MB (gt)

• BF = FD (gt)

Do đó MF // AD; $MF = \;\frac{1}{2}AD$ (định lí đường trung bình của một tam giác) (5)

* Xét ΔACD có:

• AE = EC (gt)

• CP = PD (gt)

Do đó PE // AD; EP = $\frac{1}{2}$AD (định lí đường trung bình của một tam giác) (6)

Từ (5) và (6) suy ra MF // PE // AD; $MF = PE = \;\frac{1}{2}AD$.

* Xét Δ ACB có:

• AE = EC (gt)

• AM = MB (gt)

Do đó ME // BC; $ME = \;\frac{1}{2}BC$ (định lí đường trung bình của một tam giác) (7)

* Xét ΔBDC có:

• BF = FD (gt)

• DP = PC (gt)

Do đó PF // BC; $PF = \;\frac{1}{2}BC$ (định lí đường trung bình của một tam giác) (8)

Từ (7) và (8) suy ra ME // PF // BC; $ME = PF = \;\frac{1}{2}BC$. 

c) Xét tứ giác MEPF có:

MN = PQ (chứng minh trên); NP = MQ (chứng minh trên)

Do đó, tứ giác MEPF là hình bình hành (dấu hiệu nhận biết).

Xét tứ giác MNPQ có:

MF = PE (chứng minh trên); ME = PF (chứng minh trên).

Vậy tứ giác MNPQ là hình bình hành (dấu hiệu nhận biết).