Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và $\widehat{OAD}=\widehat{OCB}$. Chứng minh tứ giác ABCD là hình bình hành.

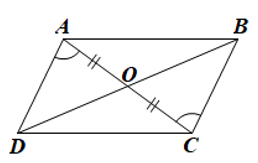
• Xét ΔOAD và ΔOCB có:

$\widehat{OAD}=\widehat{OCB}$ (giả thiết);

OA = OC (giả thiết);

$\widehat{AOD}=\widehat{COB}$ (đối đỉnh)

Do đó ΔOAD = ΔOCB (g.c.g)

Suy ra OD = OB (hai cạnh tương ứng)

• Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường

Do đó ABCD là hình bình hành.