Cho tứ giác ABCD có \(\widehat B = \widehat D = 90^\circ \).

a) CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.

b) So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD

Lời giải

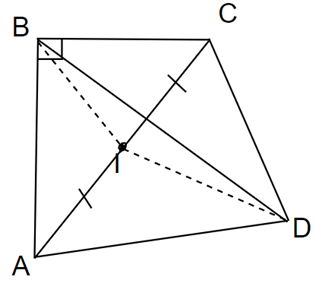
a) Gọi I là trung điểm của AC.

Xét tam giác vuông BAC có BI là đường trung tuyến

\( \Rightarrow BI = \frac{1}{2}AC\)

Þ BI = IA = IC (1)

Xét tam giác vuông DAC có DI là đường trung tuyến

\( \Rightarrow DI = \frac{1}{2}AC\)

Þ DI = IA = IC (2)

Từ (1) và (2) Þ IA = IB = IC = ID.

Vậy 4 điểm A, B, C, D cùng thuộc 1 đường tròn là đường tròn tâm I và bán kính là AI.

b) Xét tam giác BDI ta có: BI + ID > BD (theo bất đẳng thức tam giác).

Mà \(BI + ID = \frac{1}{2}AC + \frac{1}{2}AC = AC\).

Vậy AC > BD.

Để AC = BD thì BD cũng là đường kính của đường tròn ngoại tiếp tứ giác ABCD.

Khi đó ABCD là hình chữ nhật.