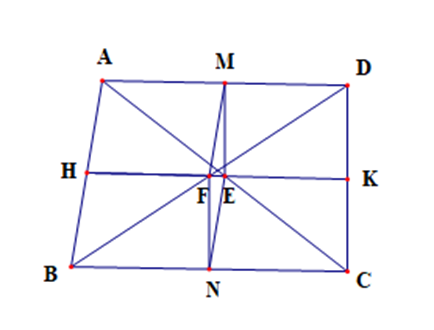
Gọi M là trung điểm của AD, N là trung điểm của BC

Xét tam giác ACD có M, E lần lượt là trung điểm của AD, AC

Suy ra ME là đường trung bình

Do đó ME // CD, $ME = \frac{1}{2}C{\rm{D}}$ (1)

Xét tam giác BCD có N, F lần lượt là trung điểm của BC, BD

Suy ra NF là đường trung bình

Do đó NF // CD, $NF = \frac{1}{2}C{\rm{D}}$  (2)

Xét tam giác ACB có N, E lần lượt là trung điểm của BC, AC

Suy ra NE là đường trung bình

Do đó NE // AB, $NE = \frac{1}{2}AB$    (3)

Xét tam giác ABD có M, F lần lượt là trung điểm của AD, BD

Suy ra MF là đường trung bình

Do đó MF // AB, $MF = \frac{1}{2}AB$   (4)

Từ (1), (2), (3) và (4) suy ra $\left\{ \begin{array}{l}ME//NF//C{\rm{D}}\\MF//NE//AB\\ME = NF = \frac{1}{2}C{\rm{D}}\\MF = NE = \frac{1}{2}AB\end{array} \right.$

Mà AB = CD nên NF = NE

Suy ra tam giác NFE cân tại N

Do đó $\widehat {NF{\rm{E}}} = \widehat {{\rm{NEF}}}$

Vì NE // AB nên $\widehat {KHB} = \widehat {NEK}$ (hai góc đồng vị)

Vì NF // CD nên $\widehat {HKC} = \widehat {NFH}$ (hai góc đồng vị)

Suy ra $\widehat {KHB} = \widehat {HKC}$

Vậy $\widehat {KHB} = \widehat {HKC}$.