Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường h
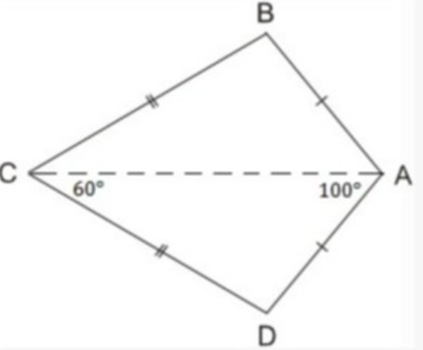
Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)
a) Chứng minh AC là đường trung trực của BD
b) Tính góc B và góc D (biết ˆA=100∘,ˆC=60∘).