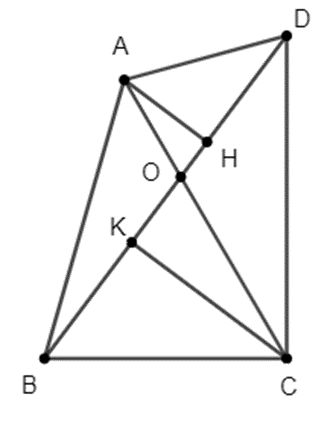
Gọi O là giao điểm hai đường chéo AC và BD và $\widehat {AOD} = \widehat {BOC} = a < 90^\circ$

Kẻ AH và CK vuông góc với BD. Ta có:

${S_{ABCD}} = {S_{ABD}} + {S_{BCD}} = \frac{1}{2}.BD.AH + \frac{1}{2}.BD.CK$

$= \frac{1}{2}.BD.\left( {AH + CK} \right)$ (1)

Lại có AH = OA.sina; CK = OC.sina

Do đo AH + CK = (OA + OC).sina = AC.sina (2)

Từ (1) và (2) suy ra ${S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a$