Cho tứ giác ABCD có 2 góc đối bù nhau. Gọi O là giao điểm 2 đường chéo AC
Cho tứ giác ABCD có 2 góc đối bù nhau. Gọi O là giao điểm 2 đường chéo AC và BD. E là giao điểm 2 đường thẳng AD và BC. Chứng minh AE.CD = CE.AB và^ABD= ^DCA.
Cho tứ giác ABCD có 2 góc đối bù nhau. Gọi O là giao điểm 2 đường chéo AC và BD. E là giao điểm 2 đường thẳng AD và BC. Chứng minh AE.CD = CE.AB và^ABD= ^DCA.
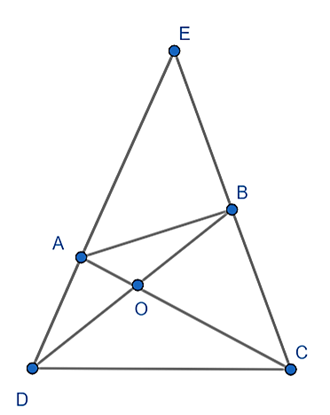
Theo bài ra ta có: ^ABC+^ADC=180∘
Mà ^ABC+^ABE=180∘(kề bù)
Suy ra: ^ABE=^ADC=^EDC
Xét ∆ABE và ∆CDE có:
Chung ˆE
^ABE=^EDC
⇒ ∆ABE ~∆CDE (g.g)
⇒ AECE=ABCD hay AE.CD = CE.AB
+) Tứ giác ABCD có 2 góc đối bù nhau nên tứ giác ABCD nội tiếp
Suy ra: ^ABD= ^DCA(cùng chắn cung AD).