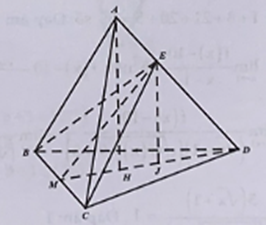
Cho tứ diện đều ABCD cạnh A. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc giữa hai mặt phẳng (P) và (BCD) có số đo là $\text{α}$ thỏa mãn $\text{tan α = }\frac{5\sqrt{2}}{7}$. Gọi thể tích của hai tứ diện ABCE và tứ diện BCDE lần lượt là V₁ và V₂. Tính tỉ số $\frac{V_1}{V_2}$.

Gọi H, I lần lượt là hình chiếu vuông góc của A, E trên mặt phẳng (BCD). Khi đó $\text{H},\text{I}\in \text{DM}$ với M là trung điểm BC. Ta tính được $\text{AH}=\frac{\text{a}\sqrt{6}}{3},\text{DH}=\frac{\text{a}\sqrt{3}}{3},\text{MH}=\frac{\text{a}\sqrt{3}}{6}$.

Ta có góc giữa (P) với $\left(\text{BCD}\right)=\widehat{\text{EMD}}=\text{α}\Rightarrow \tan \text{α}=\frac{\text{EI}}{\text{MI}}=\frac{5\sqrt{2}}{7}$

Gọi $DE=x\Rightarrow \frac{DE}{AD}=\frac{EI}{AH}=\frac{DI}{DH}\Rightarrow EI=\frac{DE.AH}{AD}=\frac{x.\frac{a\sqrt{6}}{3}}{a}=\frac{x\sqrt{6}}{3}\text{. }$

$\text{DI}=\frac{\text{DE.DH}}{\text{AD}}=\frac{\text{x.}\frac{\text{a}\sqrt{3}}{3}}{\text{a}}=\frac{\text{x}\sqrt{3}}{3}\Rightarrow \text{MI}=\text{DM}-\text{DI}=\frac{\text{a}\sqrt{3}}{2}-\frac{\text{x}\sqrt{3}}{3}$

Vậy $\tan \text{α}=\frac{EI}{MI}=\frac{5\sqrt{2}}{7}\iff \frac{\frac{x\sqrt{6}}{3}}{\frac{a\sqrt{3}}{2}-\frac{x\sqrt{3}}{3}}=\frac{5\sqrt{2}}{7}\iff x=\frac{5}{8}a$.