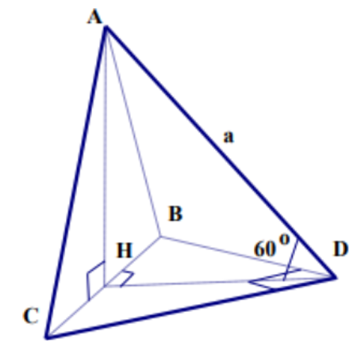
Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D, và AD hợp với (BCD) một góc 60°. Tính thể tích tứ diện ABCD.
Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D, và AD hợp với (BCD) một góc 60°. Tính thể tích tứ diện ABCD.