Cho tam giác OAB vuông tại A, OA = 3 cm, AB = 4 cm, đường cao AH (H thuộc OB)

a) Tính AH.

b) Vẽ đường tròn (O; OA) cắt tia AH tại C. Chứng minh: CB là tiếp tuyến của đường tròn (O; OA).

a)

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH ta có:

\(\frac{1}{{A{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}} \Rightarrow A{H^2} = \frac{{144}}{{25}} \Rightarrow AH = \frac{{12}}{5} = 2,4\) (cm)

b)

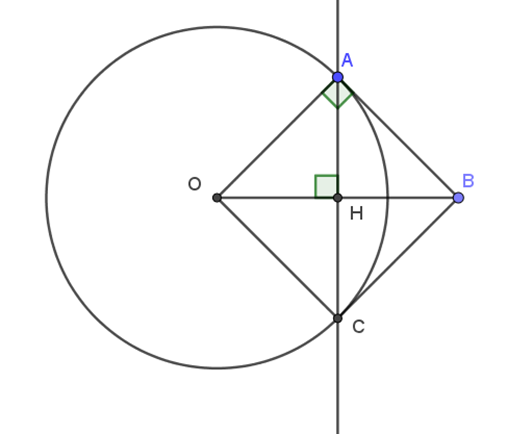
Xét đường tròn O có: OH là một phần đường kính, AC là dây cung, OH vuông góc với AC tại H nên H là trung điểm của AC

Do đó, OB là đường trung trực của AC nên ta có: AB = CB

Xét tam giác OAB và tam giác OCB có:

AB = CB

OB chung

OA = OB (cùng bằng bán kính)

Do đó, tam giác OAB bằng tam giác OCB

Do đó, ta có: \(\widehat {OCB} = \widehat {OAB} = 90^\circ \)

Vậy BC vuông góc với bán kính OC nên BC là tiếp tuyến của đường tròn tâm O