Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:

a) BC // DE.

b) Tứ giác BCED là hình thang cân.

Lời giải

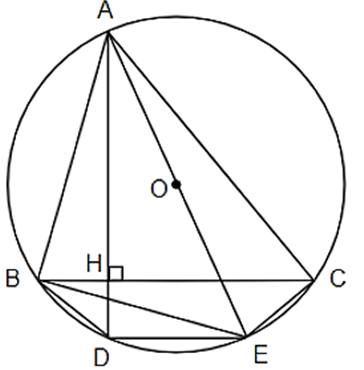
a) Xét ∆ADE nội tiếp đường tròn đường kính AE

Þ AD ^ DE          (1)

Lại có AH ^ BC Þ AD ^ BC   (2)

Từ (1) và (2) suy ra DE // BC (cùng vuông góc với AD).

b) Ta có: Tứ giác ABDC nội tiếp

\( \Rightarrow \widehat {ADB} = \widehat {ACB}\) (3) (Hai góc nội tiếp cùng chắn cung AB)

Lại có \(\widehat {ACE} = 90^\circ \) (Góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \widehat {ACB} + \widehat {BCE} = 90^\circ \) (4)

AD ^ BC \( \Rightarrow \widehat {BHD} = 90^\circ \Rightarrow \widehat {HBD} + \widehat {HDB} = 90^\circ \)

\( \Rightarrow \widehat {CBD} + \widehat {ADB} = 90^\circ \) (5)

Từ (3), (4) và (5) nên suy ra \(\widehat {BCE} = \widehat {CBD}\).

Mà BC // DE (cmt).

Nên suy ra tứ giác BCED là hình thang cân.