Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F ∈ AB) và kẻ HE ⊥ vói AC (E ∈ AC). a) Chứng minh: góc AFE = góc ACB. b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng m
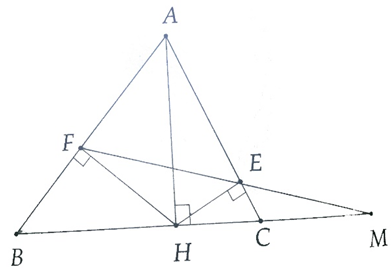
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F ∈ AB) và kẻ HE ⊥ vói AC (E ∈ AC).
a) Chứng minh: ^AFE=^ACB.
b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng minh ME . MF = MB . MC.