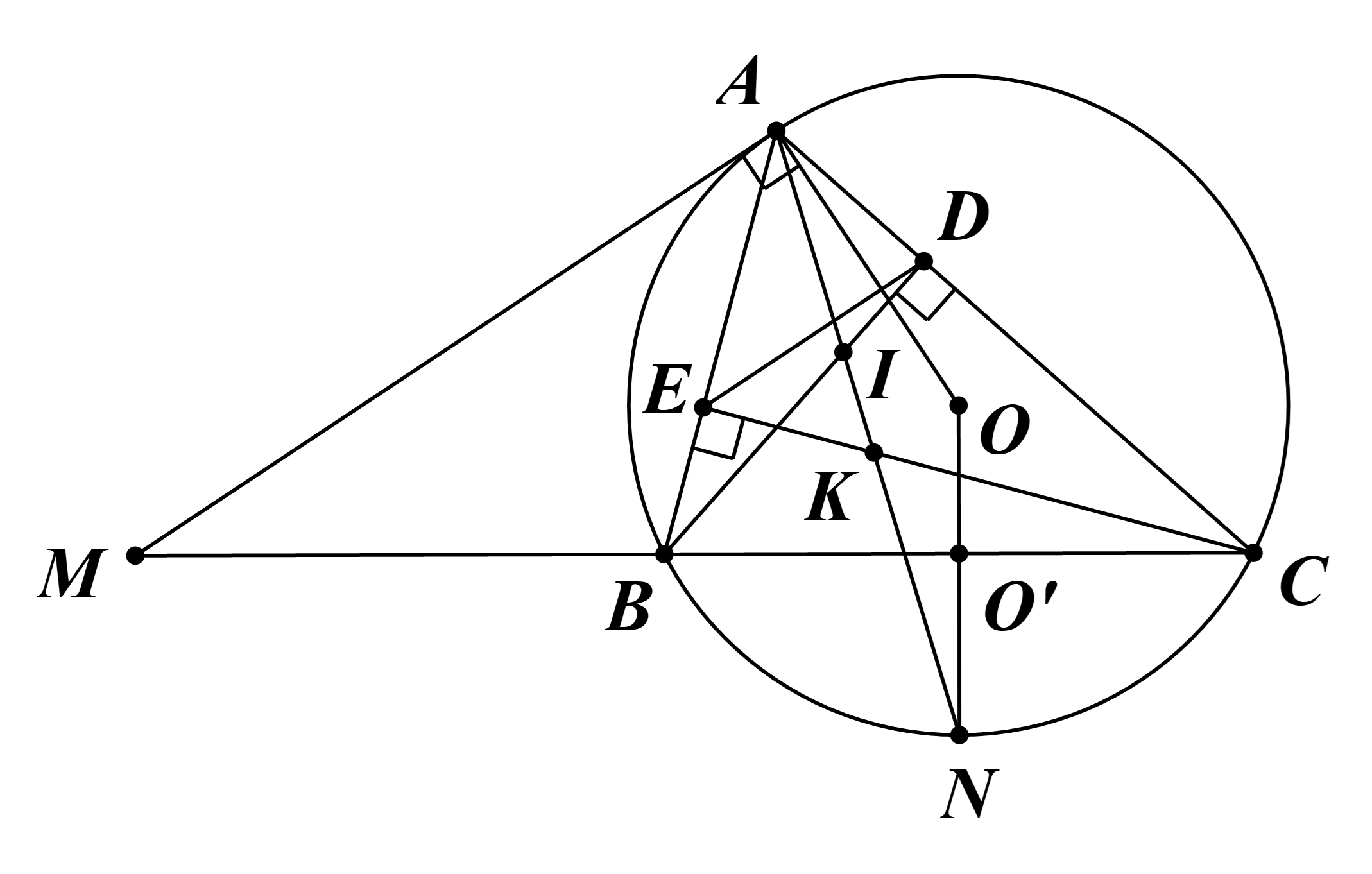
Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M. a) Chứng minh MA^2 = MB.MC. b) Vẽ đường cao BD của tam giác ABC.
Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M.
a) Chứng minh MA2 = MB.MC.
b) Vẽ đường cao BD của tam giác ABC. Đường thẳng qua D và song song với MA cắt AB tại E. Chứng minh tứ giác BCDE nội tiếp và xác định tâm O’ của đường tròn ngoại tiếp.
c) Tia OO’ cắt đường tròn (O) tại N. Chứng minh AN là tia phân giác của góc BAC.
d) Gọi I, K lần lượt là giao điểm của AN với BD và CE. Tìm điều kiện của tam giác ABC để có IBID.KCKE=IBID+KCKE.