Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt cạnh AC, AB lần lượt tại D và E. H là giao điểm của BD và CE, K là giao điểm của DE và AH, F là giao điểm của AH và BC. M l

Trả lời

Lời giải

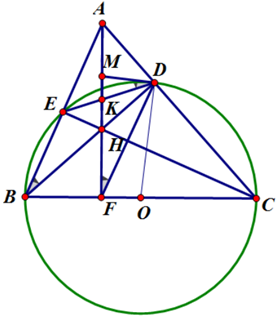
Ta có \[\widehat {BDC} = \widehat {BEC}\] = 90° (góc nội tiếp chắn nửa đường tròn).

Vì BD và CE là đường cao của ∆ABC mà BD và CE cắt nhau tại H nên H là trực tâm của ∆ABC.

Suy ra  AH ⊥ BC hay\[\widehat {AFB} = \widehat {ADB}\]= 90°.

Do đó, đỉnh D, F cùng nhìn A, B dưới góc 90°.

Suy ra tứ giác ABFD nội tiếp ⇒ \[\widehat {ABD} = \widehat {AFD}\] (góc nội tiếp cùng chắn cung AD).

Lại có ∆ADH vuông tại D; M là trung điểm của AH.

⇒ DM là đường trung tuyến ứng cạnh huyền

⇒ DM = AM

⇒ \[\widehat {MAD} = \widehat {MDA}\]

Mà OD = OC nên ∆ODC cân suy ra \[\widehat {OCD} = \widehat {ODC}\]

Do đó \[\widehat {OCD} = \widehat {MAD} = \widehat {MDA} + \widehat {ODC}\].

Do AF⊥BC ⇒ \[\widehat {MAD} + \widehat {ODC} = 90^\circ \]

⇒ \[\widehat {MDA} + \widehat {ODC} = 90^\circ \]⇒ \[\widehat {MDO} = 90^\circ \] ⇒ MD là tiếp tuyến của (O)

⇒ \[\widehat {ABF} + \widehat {MDE}\] (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây chắn cung
ED).
⇒ \[\widehat {AFD} + \widehat {MDE}\] ⇒ MDK ᔕ ∆MFD (g.g).

⇒ \[\frac{{MD}}{{MF}} = \frac{{MK}}{{MD}}\] ⇒ MD² = MK . MF.