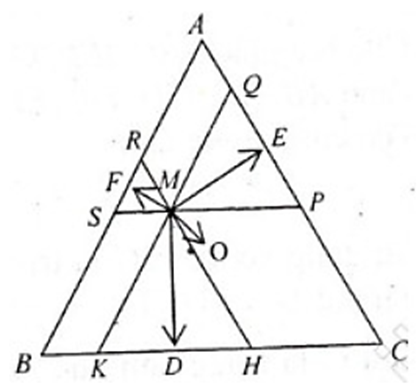
Qua M kẻ các đường thẳng song song với các cạnh của tam giác QK // AB; RH // AC; SP // BC.

Dễ thấy các tam giác MKH; MRS; MPQ đều là các tam giác đều.

Ta lại có MD ⊥ HK nên D cũng là trung điểm thuộc cạnh HK của tam giác MHK.

Ta có: \(2\overrightarrow {MD} = \overrightarrow {MH} + \overrightarrow {MK} \)

Tương tự: \(2\overrightarrow {ME} = \overrightarrow {MP} + \overrightarrow {MQ} \); \(2\overrightarrow {MF} = \overrightarrow {MR} + \overrightarrow {MS} \)

⇒ \(2\left( {\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} } \right) = \left( {\overrightarrow {MQ} + \overrightarrow {MR} } \right) + \left( {\overrightarrow {MP} + \overrightarrow {MH} } \right) + \left( {\overrightarrow {MS} + \overrightarrow {MK} } \right)\)

Tứ giác MRQA là hình bình hành nên \(\overrightarrow {MQ} + \overrightarrow {MR} = \overrightarrow {MA} \)

Tương tự: \(\overrightarrow {MP} + \overrightarrow {MH} = \overrightarrow {MC} ;\,\,\overrightarrow {MS} + \overrightarrow {MK} = \overrightarrow {MB} \)

⇒ \(2\left( {\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} } \right) = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \)

Vì O là trọng tâm của tam giác ABC và M là một điểm bất kì nên

\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MO} \)

⇒ \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)

Vậy hệ thức giữa các vectơ \(\overrightarrow {MD} ,\overrightarrow {ME} ,\)\[\overrightarrow {MF} ,\]\(\overrightarrow {MO} \) là \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} .\)