Lời giải
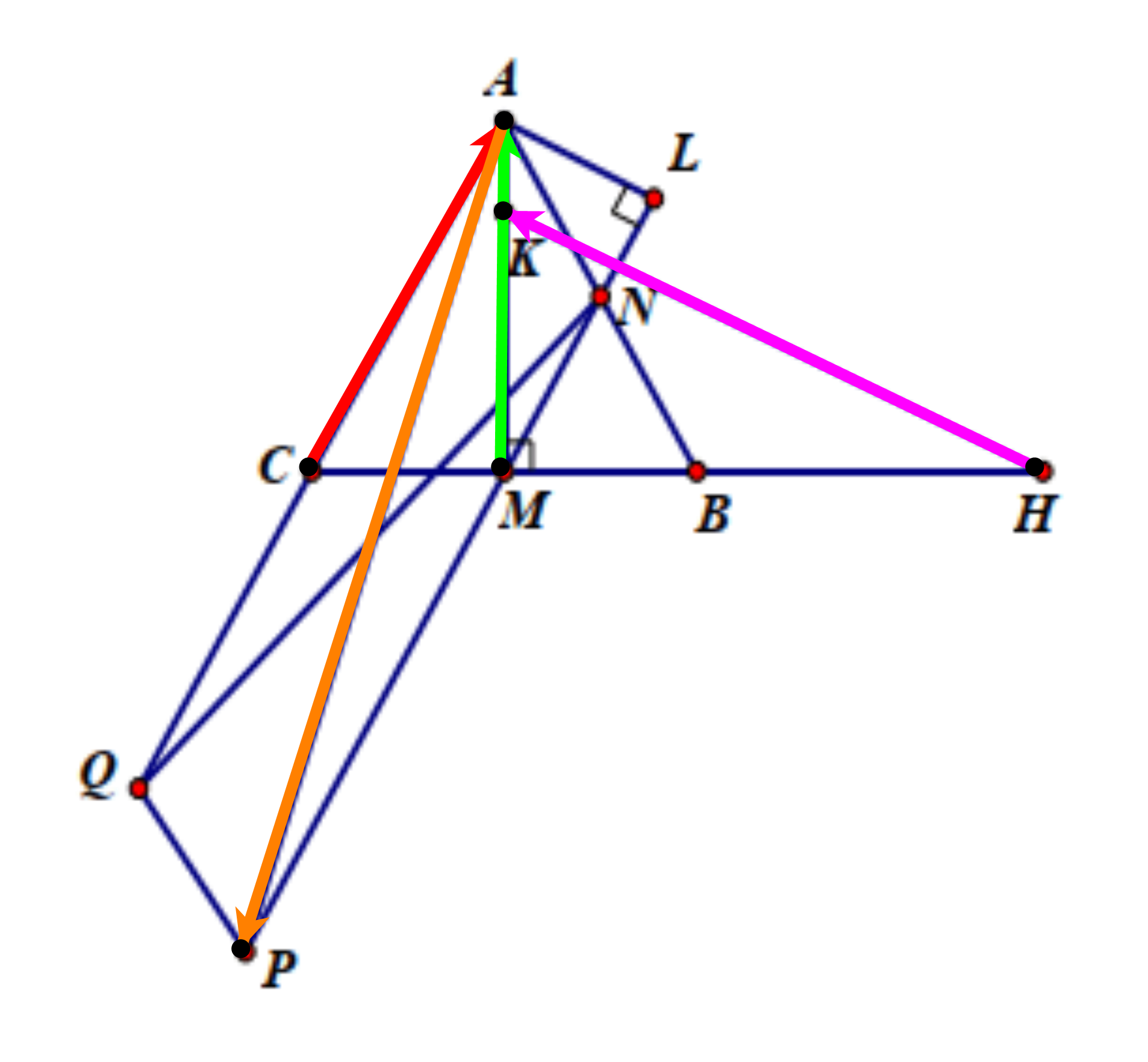
a) Ta có \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} = \overrightarrow {CM} + \overrightarrow {MA} = \overrightarrow {CA} \) (do M là trung điểm BC).
Vậy \(\left| {\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\).
b) Ta có \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} = \overrightarrow {BA} - \overrightarrow {BM} = \overrightarrow {MA} \) (do M là trung điểm BC).
Tam giác ABC đều cạnh a có M là trung điểm BC.
Suy ra \(CM = BM = \frac{{BC}}{2} = \frac{a}{2}\).
Tam giác ABC đều có AM là đường trung tuyến.
Suy ra AM cũng là đường cao của tam giác ABC.
Tam giác ACM vuông tại M: \(AM = \sqrt {A{C^2} - C{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Vậy \(\left| {\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} } \right| = \left| {\overrightarrow {MA} } \right| = MA = \frac{{a\sqrt 3 }}{2}\).
c) Ta có \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow {AN} + \overrightarrow {AQ} \), với N, C là trung điểm AB, AQ.
\( = \overrightarrow {AP} \), với P là đỉnh của hình bình hành AQPN.
Gọi L là hình chiếu của A lên PN.
Ta có MN // AC (MN là đường trung bình của ∆ABC).
Suy ra \(\widehat {ANL} = \widehat {MNB} = \widehat {ACB} = 60^\circ \).
Tam giác ANL vuông tại L:
⦁ \(\sin \widehat {ANL} = \frac{{AL}}{{AN}} \Rightarrow AL = \frac{a}{2}.\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\);
⦁ \(\cos \widehat {ANL} = \frac{{NL}}{{AN}} \Rightarrow NL = \frac{a}{2}.\cos 60^\circ = \frac{a}{4}\).
Ta có PL = PN + NL = AQ + NL = 2AC + NL \( = 2a + \frac{a}{4} = \frac{{9a}}{4}\).
Tam giác ALP vuông tại L: \(AP = \sqrt {A{L^2} + P{L^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2} + {{\left( {\frac{{9a}}{4}} \right)}^2}} = \frac{{a\sqrt {21} }}{2}\).
Vậy \(\left| {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} } \right| = \left| {\overrightarrow {AP} } \right| = AP = \frac{{a\sqrt {21} }}{2}\).
d) Gọi K là điểm nằm trên đoạn AM thỏa mãn \(MK = \frac{3}{4}MA\)và H là điểm thuộc tia MB sao cho MH = 2,5MB.
Khi đó \(\overrightarrow {MK} = \frac{3}{4}\overrightarrow {MA} ,\,\,\overrightarrow {MH} = 2,5\overrightarrow {MB} \).
Ta có \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} = \overrightarrow {MK} - \overrightarrow {MH} = \overrightarrow {HK} \).
Ta có \(MK = \frac{3}{4}MA = \frac{3}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{8}\) và \(MH = 2,5MB = 2,5.\frac{a}{2} = \frac{{5a}}{4}\).
Tam giác KMH vuông tại M: \(HK = \sqrt {M{K^2} + M{H^2}} = \sqrt {{{\left( {\frac{{3a\sqrt 3 }}{8}} \right)}^2} + {{\left( {\frac{{5a}}{4}} \right)}^2}} = \frac{{a\sqrt {127} }}{8}\).
Vậy \(\left| {\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} } \right| = \left| {\overrightarrow {HK} } \right| = HK = \frac{{a\sqrt {127} }}{8}\).
