Cho tam giác đều ABC cạnh a. a) Tính độ dài các vectơ AB + vecto CA + vecto
Cho tam giác đều ABC cạnh a.
a) Tính độ dài các vectơ →AB+→CA+→BC,→AB−→AC.
b) Xác định điểm M sao cho →AB+→AC=→AM.
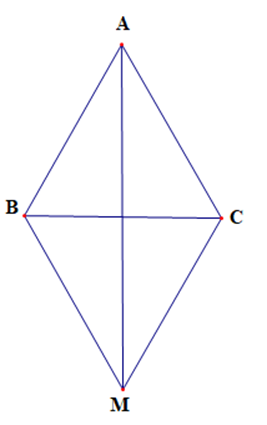
a) Ta có →AB+→CA+→BC=→AB+→BC+→CA=→AC+→CA=→0
Ta có →AB−→AC=→CB
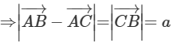
b) Vẽ hình bình hành ABMC
Suy ra →AB+→AC=→AM
Vậy M là đỉnh thứ tư của hình bình hành ABMC.