Cho tam giác ABC vuông tại C (AC < BC), đường cao CHK và đường phân giác
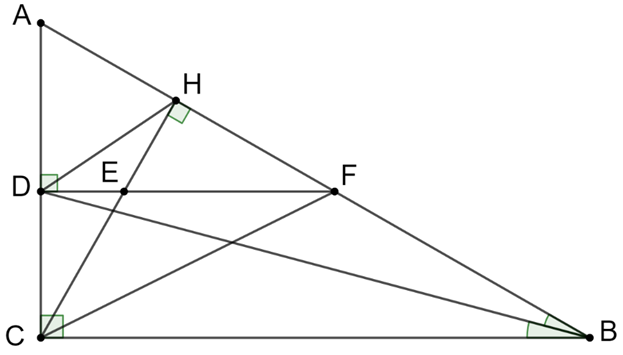
Cho tam giác ABC vuông tại C (AC < BC), đường cao CHK và đường phân giác trong BD (H Î AB, D Î AC). Qua D kẻ đường thẳng vuông góc với AC cắt CH, AB lần lượt tại E và F.
a) Chứng minh bốn điểm C, D, H, F cùng thuộc một đường tròn.
b) Chứng minh AD.AC = DE.AB