Cho tam giác ABC vuông tại A. Về phía ngoài của tam giác vẽ các hình vuông ABDE, ACGH.

a) Chứng minh tứ giác BCHE là hình thang cân.

b) Vẽ đường cao AK của tam giác ABC. Chứng minh AK, DE, GH đồng quy.

Lời giải

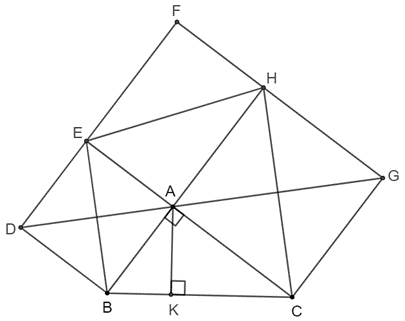
a) Vì ABDE, ACGH là hình vuông nên D, A, G thẳng hàng.

Suy ra \[\widehat {DAB} + \widehat {BAC} + \widehat {CAG} = 45^\circ + 90^\circ + 45^\circ = 180^\circ \]

Do đó BE // CH (vì cùng vuông góc với DG)

Mà AE = AB, AH = AC

Suy ra ΔAEH = ΔABC (c.g.c)

⇒ \[\widehat {AHE} = \widehat {DCB}\] (hai góc tương ứng).

⇒ \[\widehat {AHC} = \widehat {BCH}\]

⇒ Tứ giác BCHE là hình thang cân.

b) Gọi DE ∩ HG = F nên EFHA là hình chữ nhật

⇒ \[\widehat {FAE} = \widehat {HEA}\]

Mà \[\widehat {AEH} = \widehat {ABC};\,\,\widehat {ABC} = \widehat {KAC}\] nên \[\widehat {FAE} = \widehat {KAC}\].

Do đó F, A, K thẳng hàng.

Vậy AK, DE, GH đồng quy.