Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ HD vuông AC, HE vuông AB. Gọi M, N lần lượt là trung điểm của các đoạn thẳng HB, HC. Chứng minh tứ giác DEMN là hình thang vuông.
40
18/05/2024
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ HD vuông AC, HE vuông AB. Gọi M, N lần lượt là trung điểm của các đoạn thẳng HB, HC. Chứng minh tứ giác DEMN là hình thang vuông.
Trả lời
Lời giải
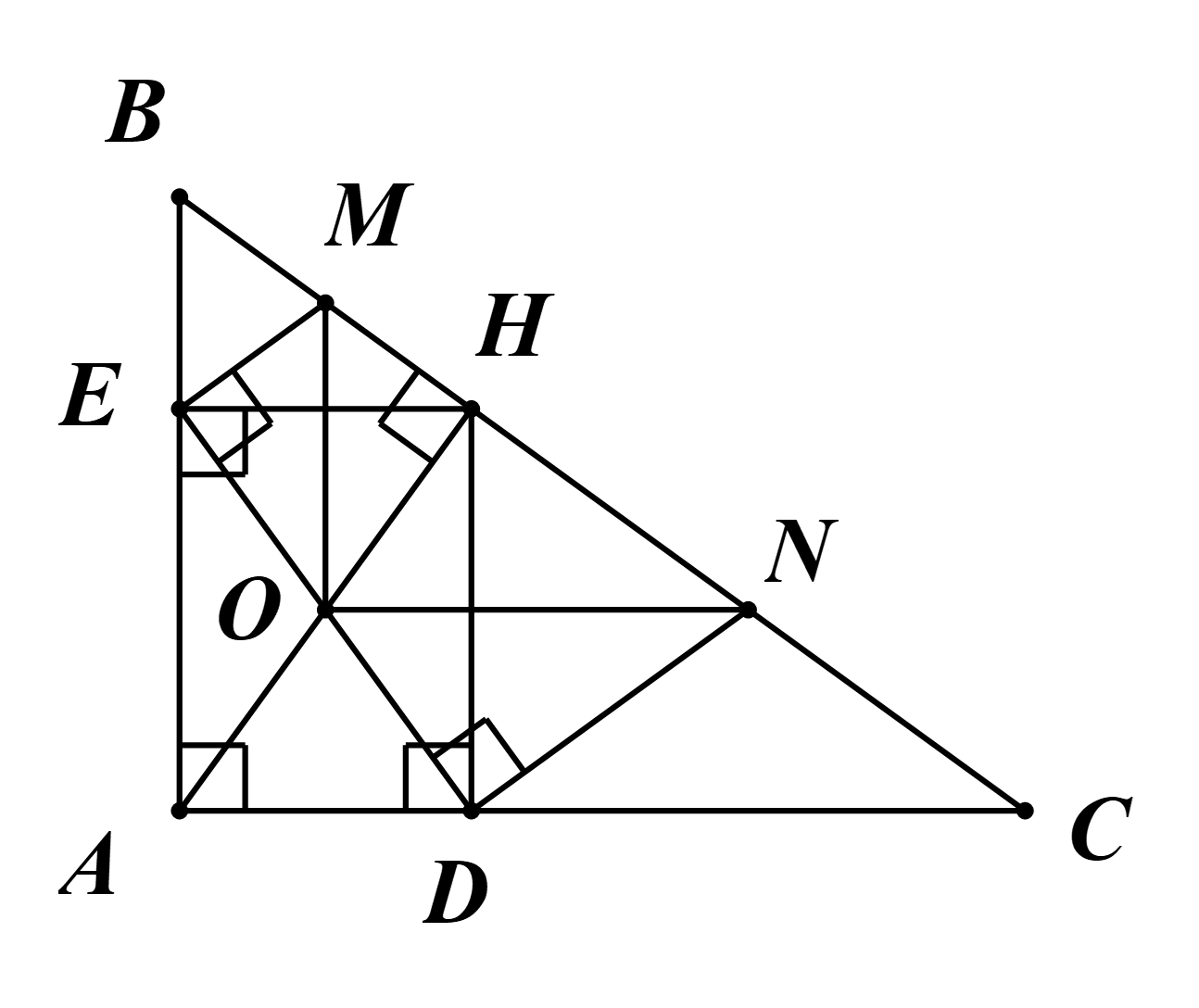
Ta có \(\widehat {HEA} = \widehat {EAD} = \widehat {ADH} = 90^\circ \).
Suy ra tứ giác AEHD là hình chữ nhật.
Do đó ED = AH.
Gọi O là giao điểm của ED và AH.
Suy ra OE = OH = OA = OD.
Tam giác BEH vuông tại E có EM là đường trung tuyến.
Suy ra EM = MH.
Xét ∆MEO và ∆MHO, có:
MO là cạnh chung;
ME = MH (chứng minh trên);
OE = OH (chứng minh trên).
Do đó ∆MEO = ∆MHO (c.c.c).
Suy ra \(\widehat {MEO} = \widehat {MHO} = 90^\circ \) (cặp góc tương ứng).
Vì vậy ME ⊥ DE (1)
Chứng minh tương tự, ta được DN ⊥ DE (2)
Từ (1), (2), suy ra ME // DN.
Ta có ME // DN (chứng minh trên) và \(\widehat {MED} = \widehat {EDN} = 90^\circ \) (chứng minh trên).
Vậy tứ giác DEMN là hình thang vuông.

