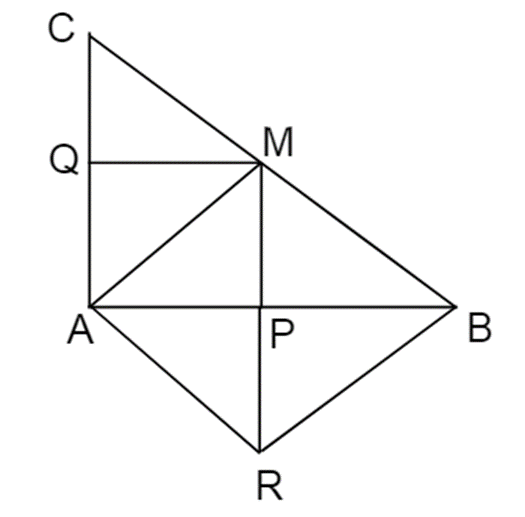
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB
Cho ΔABCvuông tại A. Gọi M là trung điểm của BC. Từ M hạ MP vuông góc với AB, P∈AB, MQ⊥AC(Q∈AC) R đối xứng M qua P
a, AQMP là hình gì ? Vì sao?
b, AMBR là hình gì ? Vì sao?
c, Điều kiện để tâm giác ANG để AQM P là hình vuông