cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.              

1) Chứng minh AD = BC.        

2) Chứng minh CD vuông góc với AC.          

3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.

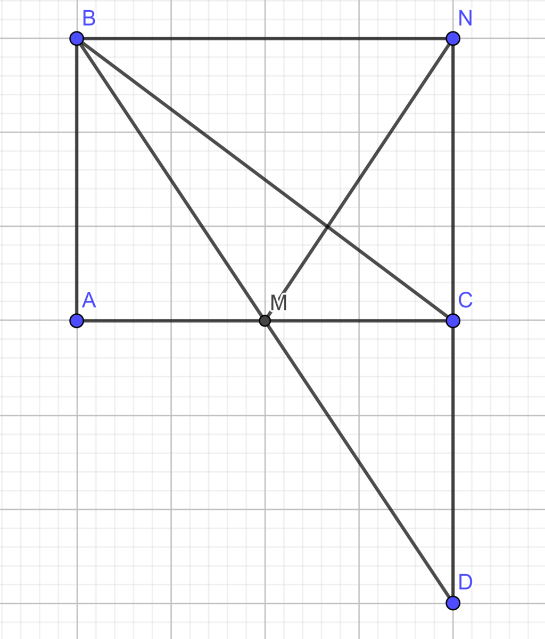
1) Xét ΔCBM và ΔADM có:

AM = MC (giả thtết)

 $\widehat{CMB}=\widehat{AMD}$( đối đỉnh)

BM = MD (giả thiết)

⇒ ΔCBM = ΔADM (c.g.c)

Suy ra: BC = DA (hai cạnh tương ứng)

2) Xét ΔABM và ΔCDM có:

AM = CM (giả thiết)

 $\widehat{CMD}=\widehat{AMB}$(đối đỉnh)

BM = DM (giả thiết)     

⇒ ΔABM = ΔCDM (c.g.c)

$\widehat{BAM}=\widehat{DCM}$= 90°(hai góc tương ứng) (đpcm)

⇒ DC⊥AC (đpcm)

3) Ta có BN // AC mà AC ⊥ DC ⇒ BN ⊥ DC ⇒ $\widehat{BND}$ = 90°

AB // CD (do cùng ⊥AC)

Xét ΔABC và ΔNBC có:

$\widehat{ABC }=\widehat{NCB}$ (hai góc ở vị trí so le trong)

BC chung

$\widehat{ACB }=\widehat{NBC}$(do BN//AC nên đó là hai góc ở vị trí so le trong)

⇒ ΔABC = ΔNBC (g.c.g)

⇒ AB = NC (hai cạnh tương ứng)

Xét ΔABM và ΔCNM có:

AB = CN (cmt)

$\widehat{BAM}=\widehat{NCM}$= 90°

AM = CM (giả thiết)

⇒ ΔABM = ΔCNM (đpcm).