Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.

a) Chứng minh AH = DE.

b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.

Lời giải

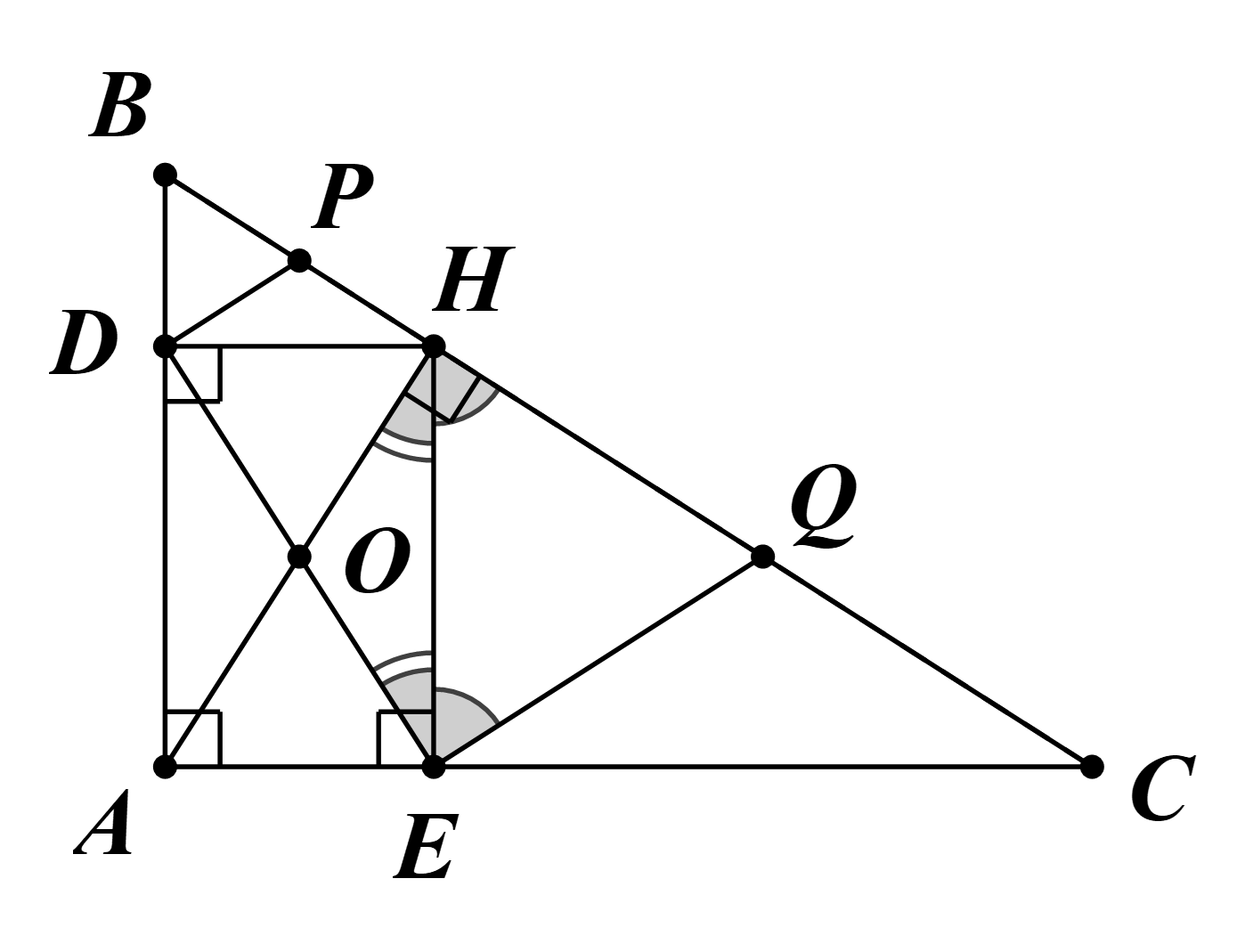
a) Tứ giác ADHE, có:

$\widehat {DAE} = 90^\circ$ (do tam giác ABC vuông tại A);

$\widehat {ADH} = 90^\circ$ (do HD ⊥ AB tại D);

$\widehat {AEH} = 90^\circ$ (do HE ⊥ AC tại E).

Do đó tứ giác ADHE là hình chữ nhật.

Vậy AH = DE.

b) Tam giác HEC vuông tại E có EQ là đường trung tuyến.

Suy ra EQ = HQ = QC.

Khi đó tam giác HEQ cân tại Q.

Vì vậy $\widehat {QEH} = \widehat {QHE}$   (1)

Hình chữ nhật ADHE có O là giao điểm của hai đường chéo AH và DE.

Suy ra O là trung điểm của AH và O cũng là trung điểm của DE.

Mà AH = DE (chứng minh trên).

Do đó OH = OE = OD = OA.

Vì vậy tam giác OHE cân tại O.

Suy ra $\widehat {OEH} = \widehat {OHE}$   (2)

Ta có AH ⊥ HQ (giả thiết).

Suy ra $\widehat {OHQ} = 90^\circ$.

Vì vậy $\widehat {OHE} + \widehat {QHE} = 90^\circ$   (3)

Từ (1), (2), (3), suy ra $\widehat {OEQ} = 90^\circ$.

Khi đó OE ⊥ EQ (*)

Chứng minh tương tự, ta được OD ⊥ DP   (**)

Từ (*), (**), suy ra PD // EQ.

Mà $\widehat {OEQ} = 90^\circ$ (chứng minh trên).

Vậy tứ giác DEQP là hình thang vuông.