Cho tam giác ABC vuông tại A đường cao AH. Gọi O và K lần lượt là giao điểm của các đường phân giác của tam giác ABH và ACH. Vẽ AD vuông góc với OK. Chứng minh rằng các đường thẳng AD, BO, CK đồng quy.
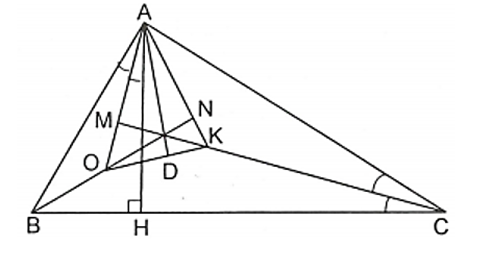
Xét tam giác ABC vuông tại A, AH vuông góc với BC nên ta có:
\(\widehat {BAH} = \widehat {ACB}\) (cùng phụ với \(\widehat {ABC}\))
Gọi M là giao điểm của AO và CK, gọi N là giao điểm của AK và BO
Vì O là giao điểm của các đường phân giác của tam giác ABH nên \(\widehat {BAO} = \widehat {HAO}\)
Vì K là giao điểm của các đường phân giác của tam giác ACH nên \(\widehat {ACK} = \widehat {BCK}\)
Xét tam giác AMC có:
\(\widehat {MAC} + \widehat {MCA} = \widehat {MAC} + \frac{{\widehat {ACB}}}{2} = \widehat {MAC} + \frac{{\widehat {BAH}}}{2} = \widehat {MAC} + \widehat {MAB} = \widehat {BAC} = 90^\circ \)
Suy ra \(\widehat {AMC} = 90^\circ \)
Do đó, CM vuông góc với AO
Chứng minh tương tự được BN vuông góc với AK
Xét tam giác AOK có AD và BO và CK là ba đường cao nên chúng đồng quy.