Lời giải
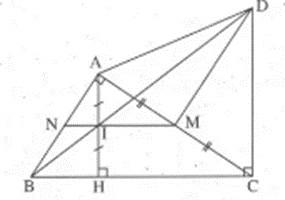
Gọi M là trung điểm của AC, N là giao điểm của IM và AB
Xét tam giác AHC có I là trung điểm của AH, M là trung điểm của AC
Suy ra IM là đường trung bình
Do đó IM // HC
Hay MN // BC
Ta có AH ⊥ BC, CD ⊥ BC nên AH // CD
Xét tam giác BCD có HI // CD
Suy ra \(\frac{{IB}}{{I{\rm{D}}}} = \frac{{HB}}{{HC}}\) (1)
Xét tam giác ABC có MN // BC (chứng minh trên)
Suy ra \(\frac{{IN}}{{HB}} = \frac{{AI}}{{HA}} = \frac{{IM}}{{HC}}\)
Hay \(\frac{{IN}}{{IM}} = \frac{{HB}}{{HC}}\) (2)
Từ (1) và (2) suy ra \(\frac{{IB}}{{I{\rm{D}}}} = \frac{{IN}}{{IM}}\)
Xét tam giác DIM có \(\frac{{IB}}{{I{\rm{D}}}} = \frac{{IN}}{{IM}}\)
Suy ra BN // DM (định lí Thales đảo)
Mà BN ⊥ AC nên DM ⊥ AC
Xét tam giác ADC có DM vừa là đường trung tuyến vừa là đường cao
Suy ra tam giác ADC cân tại D
Do đó DA = DC
Vậy DA = DC.