Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Chứng minh: AB2 = AH.BC.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Chứng minh: AB2 = AH.BC.
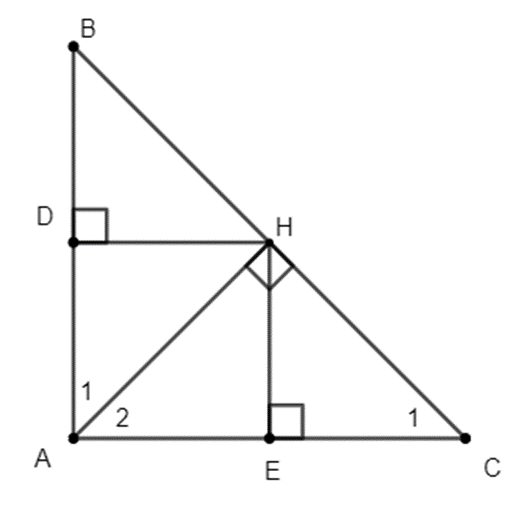
a) Xét tứ giác AEHD có: ˆA=ˆE=ˆD=90∘
Suy ra tứ giác AEHD là hình chữ nhật.
b) Xét ΔAHC có ˆH=90∘⇒^A2+^C1=90∘(1)
Xét ΔABC vuông tại A ⇒^A1+^A2=90∘(2)
Từ (1) và (2) suy ra: ^C1=^A1
Xét ΔABH và ΔCBAcó:
^C1=^A1
ˆB chung
Suy ra ΔABHᔕΔCBA.
⇒ABCB=BHBA⇔AB2=BH.CB(đpcm)