Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:

a) AB² = BH . BC;

b) AC² = CH . BC;

c) $\frac{1}{{{\rm{A}}{{\rm{H}}^2}}} = \frac{1}{{{\rm{A}}{{\rm{B}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{C}}^2}}}$.

Lời giải

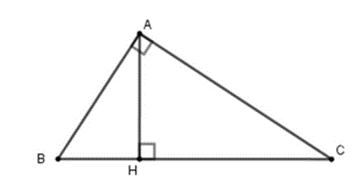
a) Xét ∆ABH và ∆CBA có:

$\widehat {BHA} = \widehat {BAC} = 90^\circ$

$\widehat {ABC}$ chung.

Do đó  (g.g)

Suy ra $\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}$ (tỉ số đồng dạng)

Do đó AB² = BH . BC.

d) Xét ∆CAH và ∆CBA có:

$\widehat {CHA} = \widehat {BAC} = 90^\circ$.

$\widehat {ACB}$ chung.

Do đó  (g.g)

Suy ra $\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}$ (tỉ số đồng dạng)

Do đó AC² = CH . BC.

c) Ta có $\frac{1}{{{\rm{A}}{{\rm{B}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{C}}^2}}} = \frac{1}{{{\rm{BH}}{\rm{.BC}}}} + \frac{1}{{{\rm{CH}}{\rm{.BC}}}}$

                                  $= \frac{{{\rm{CH}}{\rm{.BC}}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}} + \frac{{{\rm{BH}}{\rm{.BC}}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}}$

                                  $= \frac{{{\rm{CH}}{\rm{.BC + BH}}{\rm{.BC}}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}}$

                                  $= \frac{{{\rm{BC(CH + BH)}}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}} = \frac{{{\rm{BC}}{\rm{. BC}}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}}$

                                  $= \frac{{{\rm{B}}{{\rm{C}}^2}}}{{{\rm{CH}}{\rm{.BH}}{\rm{.B}}{{\rm{C}}^2}}} = \frac{1}{{{\rm{CH}}{\rm{.BH}}}}$.

Vì tam giác AHC vuông tại H nên $\widehat {HCA} + \widehat {HAC} = 90^\circ$(trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Mà $\widehat {BAH} + \widehat {HAC} = \widehat {BAC} = 90^\circ$

Suy ra $\widehat {BAH} = \widehat {HCA}$

Xét ∆AHB và ∆CHA có:

$\widehat {BHA} = \widehat {AHC} = 90^\circ$

$\widehat {BAH} = \widehat {HCA}$(chứng minh trên)

Do đó  (g.g)

Suy ra $\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}$ (tỉ số đồng dạng)

Do đó AH² = BH . CH.

Vậy $\frac{1}{{{\rm{A}}{{\rm{B}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{C}}^2}}}$= $\frac{1}{{{\rm{CH}}{\rm{.BH}}}}$= $\frac{1}{{{\rm{A}}{{\rm{H}}^2}}}$.