Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 9cm ; AC=12cm

a) Tính số đo góc B (làm tròn đến độ) và độ dài BH

b) Gọi E, F là hình chiếu của H trên AB, AC. Chứng minh AE.AB = AF.AC.

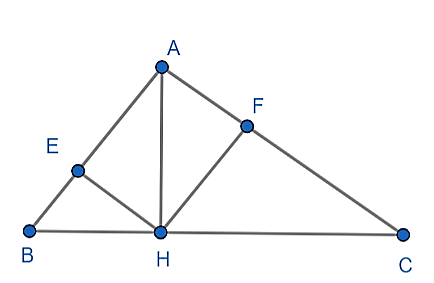
a) Theo định lí Pytago, ΔABC vuông tại A có:

BC² = AB² + AC² = 9² + 12² = 225

⇔ BC = 15(cm)

Từ đó, ta có:

sin B = $\frac{AC}{BC}=\frac{12}{15}$  = 0,8

⇔ $\widehat{B}=53°$

Theo hệ thức lượng: AB² = BH.BC

⇔ BH = $\frac{A{B}^2}{BC}$  = $\frac{9^2}{15}$= 5,4(cm)

b) AH ⊥ BC tại H ⇔ ΔABH, ΔACH vuông tại H

E là hình chiếu của H trên AB

⇔ HE ⊥ AB

⇔ HE là đường cao ΔABH

Suy ra: AH² = AE.AB (1)

F là hình chiếu của H trên AC

⇔ HF ⊥ AC

⇔ HF là đường cao ΔACH

Suy ra: AH² = AF.AC (2)

Từ (1) và (2), ta có: AE.AB = AF.AC