Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.

a) So sánh độ dài AM, DE.

b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.

Lời giải

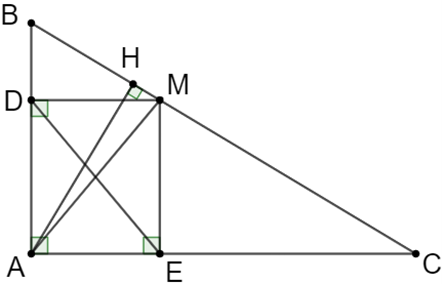
a) Tam giác ABC vuông tại A \( \Rightarrow \widehat {BAC} = 90^\circ \Rightarrow \widehat {DAE} = 90^\circ \).

• MD ^ AB \( \Rightarrow \widehat {MDA} = 90^\circ \);

• ME ^ AC \( \Rightarrow \widehat {MEA} = 90^\circ \).

Tứ giác ADME có: \(\widehat {DAE} = \widehat {MDA} = \widehat {MEA} = 90^\circ \) nên suy ra ADME là hình chữ nhật.

Hình chữ nhật ADME có AM và DE là hai đường chéo nên AM = DE.

b) Kẻ AH vuông góc với BC

Tam giác AHM vuông tại H nên AM ≥ AH (cạnh góc vuông bé hơn cạnh huyền).

Lại có DE = AM (ADME là hình chữ nhật)

Þ DE ≥ AH.

Dấu "=" xảy ra khi M ≡ H.

Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường cao kẻ từ A đến BC.