Cho tam giác ABC vuông tại A có góc ABC = 60^0 và AB = 8 cm. Kẻ đường cao AH (H thuộc cạnh BC). Tính AH, AC, BC
Cho tam giác ABC vuông tại A có ^ABC=60∘ và AB = 8 cm. Kẻ đường cao AH (H thuộc cạnh BC). Tính AH, AC, BC
Lời giải
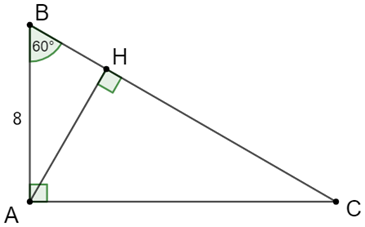
Ta có:
• cosB=ABBC⇒BC=ABcosC=8cos60∘=16(cm);
• AB=√BC2−AB2=√162−82=8√3(cm);
• AH.BC=AB.AC⇔AH=AB.ACBC=8.8√316=4√3(cm)