Cho tam giác ABC vuông tại A có đường cao AH.

Chứng minh rằng: $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$.

Lời giải

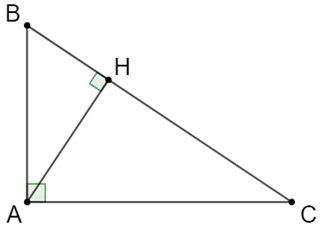
Do ∆ABC là tam giác vuông tại A nên:

${S_{ABC}} = \frac{{AH.BC}}{2} = \frac{{AB.AC}}{2} \Rightarrow AH.BC = AB.AC$

$\Leftrightarrow AH = \frac{{AB.AC}}{{BC}} \Leftrightarrow \frac{1}{{AH}} = \frac{{BC}}{{AB.AC}}$

$\Leftrightarrow \frac{1}{{A{H^2}}} = \frac{{B{C^2}}}{{A{B^2}.A{C^2}}}$

Mặt khác theo định lý Pytago thì:

BC² = AB² + AC²

$\Rightarrow \frac{1}{{A{H^2}}} = \frac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$.

Do đó ta có đpcm.