Cho tam giác ABC vuông tại A có AB = AC. Qua A vẽ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:
a) ∆BAM = ∆ACN;
b) MN = BM + CN.
Lời giải
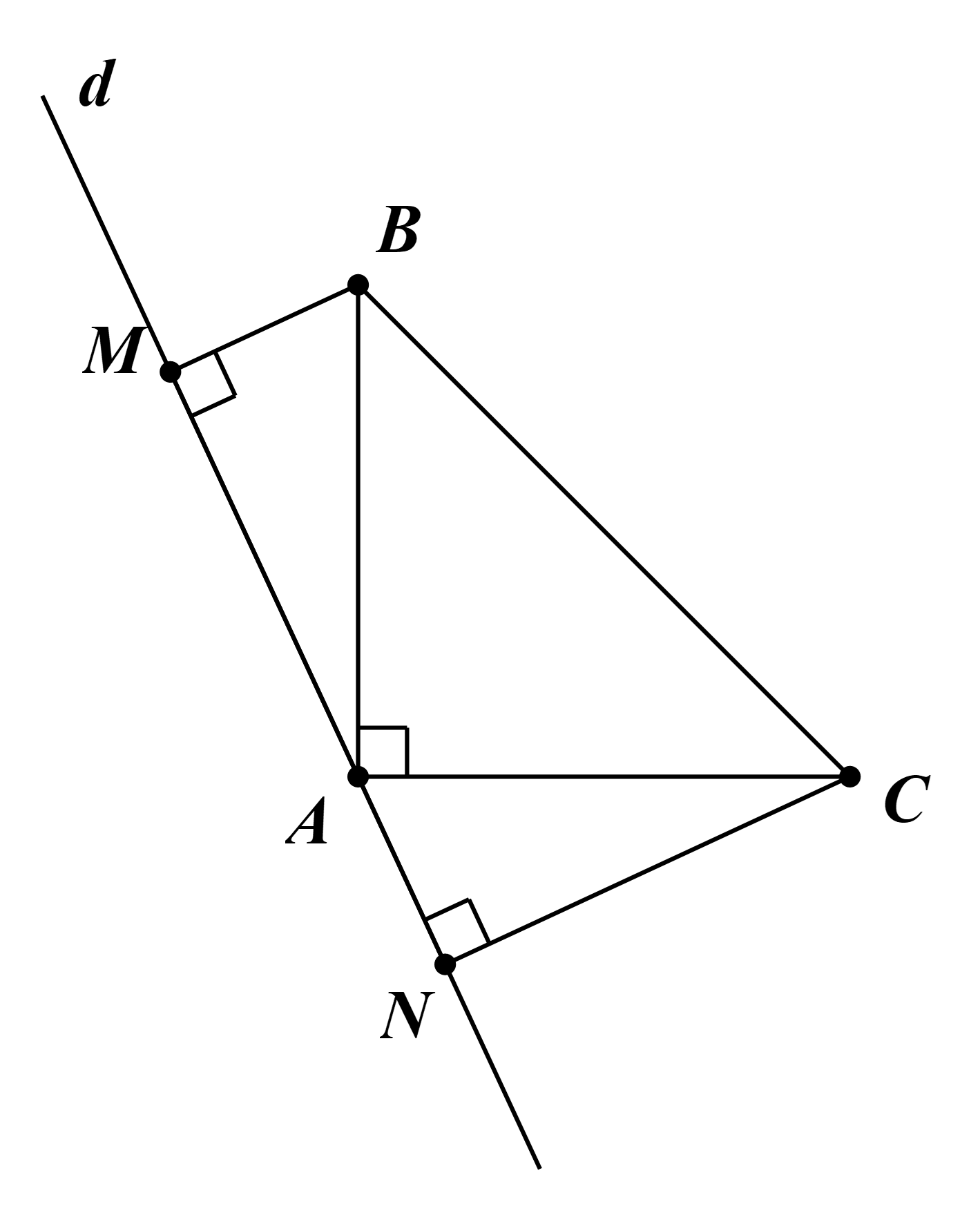
Ta có \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = 180^\circ \) (kề bù)
\( \Leftrightarrow \widehat {MAB} + \widehat {CAN} = 180^\circ - \widehat {BAC} = 180^\circ - 90^\circ = 90^\circ \).
Mà \(\widehat {MAB} + \widehat {ABM} = 90^\circ \) (do tam giác ABM vuông tại M).
Do đó \(\widehat {ABM} = \widehat {CAN}\).
Xét ∆BAM và ∆ACN, có:
\[\widehat {BMA} = \widehat {ANC} = 90^\circ \];
AB = AC (do tam giác ABC vuông cân đỉnh A);
\(\widehat {ABM} = \widehat {CAN}\) (chứng minh trên).
Do đó ∆BAM = ∆ACN (cạnh huyền – góc nhọn).
b) Ta có ∆BAM = ∆ACN (chứng minh trên).
Suy ra BM = AN và AM = CN (các cặp cạnh tương ứng).
Ta có MN = AM + AN = CN + BM.
Vậy ta có điều phải chứng minh.