Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC, điểm D thuộc AC sao cho $AD=\frac{a}{2}$. Chứng minh rằng BD vuông góc với AM.

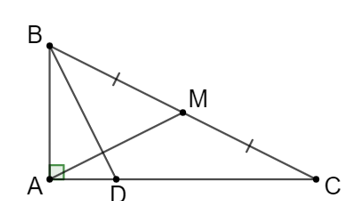
Xét tam giác ABC vuông tại A có:

AB ^ AC Û   $\overrightarrow{AB}.\overrightarrow{AC}=0\iff \overrightarrow{AB}.\overrightarrow{AD}=0$(vì D thuộc AC)

Vì M là trung điểm của BC nên ta có $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$ .

Lại có:  $\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$ (quy tắc ba điểm).

Khi đó ta có:  $2\overrightarrow{AM}.\overrightarrow{BD}$

$=\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AD}-\overrightarrow{AB}\right)$

$=\overrightarrow{AB}.\overrightarrow{AD}-{\overrightarrow{AB}}^2+\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AC}.\overrightarrow{AB}$

$=0-A{B}^2+AC.AD.\cos 0°-0$

$=-a^2+2a.\frac{a}{2}=0$.