Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.

a) Tính số đo góc B, góc C (làm tròn đến độ) và đường cao AH.

b) Chứng minh rằng: \(AB.\cos B + AC.\cos C = BC.\)

c) Trên cạnh AC lấy điểm D sao cho DC = 2DA. Vẽ DE vuông góc với BC tại E. Chứng minh rằng: \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\)

Lời giải

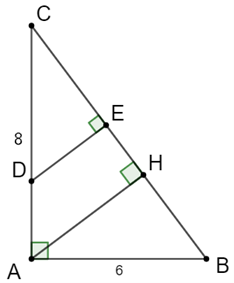
a) ∆ABC vuông tại A, đường cao AH

\( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\;cm\)

Ta có:

\(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5} \Rightarrow \widehat B = {53^ \circ } \Rightarrow \widehat C = {37^ \circ }\)

Có AH.BC = AB.AC (Hệ thức về cạnh và đường cao trong tam giác vuông)

\( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = 4,8\;cm\)

b) ∆HBA vuông tại H (AH ^ BC) Þ BH = AB.cos B

Tương tự: ∆HCA vuông tại H (AH ^ BC) Þ CH = AC.cos C

Mà BH + CH = BC Þ \(AB.\cos B + AC.\cos C = BC.\)

c) ∆ABC vuông tại A, đường cao AH

\( \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}}\) (1)

Ta có: DE // AH (cùng vuông góc với BC)

\( \Rightarrow \frac{{DE}}{{AH}} = \frac{{CD}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{D{E^2}}}{{A{H^2}}} = \frac{4}{9} \Rightarrow \frac{1}{{A{H^2}}} = \frac{4}{{9D{E^2}}}\) (2)

Từ (1) và (2) suy ra \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9D{E^2}}}\)