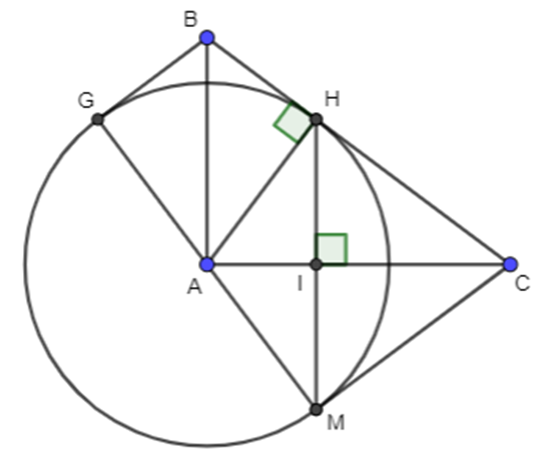
a) Áp dụng định lí Pytago vào $\Delta ABC$ vuông tại A, ta được:

$B{C^2} = A{B^2} + A{C^2}$

$\Leftrightarrow B{C^2} = {3^2} + {4^2} = 25$

hay BC = 5(cm)

Xét $\Delta ABC$ vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

$AH \cdot BC = AB \cdot AC$

$\Leftrightarrow AH \cdot 5 = 3 \cdot 4 = 12$

hay AH = 2,4(cm)

Vậy: BC = 5cm; AH = 2,4cm

b) Xét (A) có

AI là một phần đường kính

MH là dây

$AI \bot MH$ tại I(gt)

Do đó: I là trung điểm của MH(Định lí đường kính vuông góc với dây)

Xét $\Delta CMI$ vuông tại I và $\Delta CHI$ vuông tại I có

CI chung

IM = IH(I là trung điểm của MH)

Do đó:$\Delta CMI = \Delta CHI$ (hai cạnh góc vuông)

Suy ra: CM = CH(hai cạnh tương ứng)

Xét $\Delta CMA$ và $\Delta CHA$ có

CM = CH(cmt)

CA chung

AM = AH( = R)

Do đó: $\Delta CMA = \Delta CHA\left( {c - c - c} \right)$

Suy ra:$\widehat {CMA} = \widehat {CHA}$ (Hai góc tương ứng)

mà$\widehat {CHA} = {90^0}$ (gt)

nên $\widehat {CMA} = {90^0}$

hay CM là tiếp tuyến của (A)

251. có bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau và là số lẻ