Cho tam giác ABC vuông tại A. Biết AB = 12 cm, AC = 16 cm, đường phân giác AD, đường cao AH . Tính HD, HB.

Trả lời

Lời giải

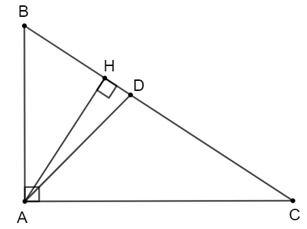
Ta có: BC² = AB² + AC²

= 12² + 16² = 400

⇒ BC = $\sqrt {400}$ = 20 (cm)

Δ ABC vuông có đường cao AH:

⇒ AB² = BH.BC

⇒ BH = $\frac{{A{B^2}}}{{BC}}$ = $\frac{{{{12}^2}}}{{20}}$ = 7,2 (cm)

⇒ CH = 20 – 7,2 = 12,8 (cm)

Ta có: AD là phân giác

⇒ $\frac{{BD}}{{CD}}$ = $\frac{{AB}}{{AC}}$

⇒ $\frac{{BD + CD}}{{CD}}$ = $\frac{{AB + AC}}{{AC}}$

⇒ $\frac{{20}}{{CD}}$ = $\frac{{28}}{{16}}$

⇒ CD = $\frac{{80}}{7}$

⇒ HD = CH – CD

= 12,8 – $\frac{{80}}{7}$ = $\frac{{48}}{{35}}$ (cm).