Cho tam giác ABC vuông tại A, AD là phân giác. Chứng minh:
Cho tam giác ABC vuông tại A, AD là phân giác. Chứng minh: \(\frac{{\sqrt 2 }}{{AD}} = \frac{1}{{AB}} + \frac{1}{{AC}}\).
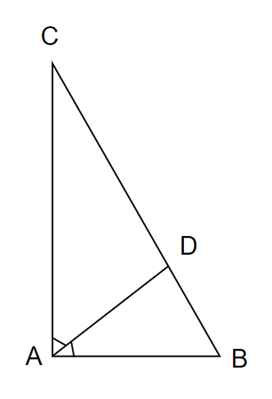
Ta có: SABC = SDAB + SDAC
\(\frac{1}{2}AB.AC = \frac{1}{2}.AB.AD.\sin 45^\circ + \frac{1}{2}.AC.AD.\sin 45^\circ = \frac{1}{2}AD.\sin 45^\circ .\left( {AB + AC} \right)\)
⇔ \(\frac{{AB + AC}}{{AB.AC}} = \frac{{\sqrt 2 }}{{AD}}\)
⇔ \(\frac{{\sqrt 2 }}{{AD}} = \frac{1}{{AB}} + \frac{1}{{AC}}\).